 |
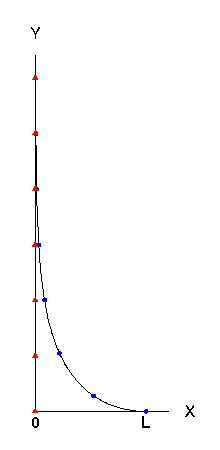
(左図の説明) ハナコちゃんは時刻 t=0 に原点 (0,0) にいる。タロウ君は時刻 t=0 に X 軸上の点 (L,0) にいる。 ハナコちゃんは Y 軸にそって歩く。時間 L/(2v) ごとのハナコちゃんの位置を赤色のマークで表した。 タロウ君は図のような曲線に沿って歩く。同じように時間L/(2v) ごとのタロウ君の位置を青色のマークで表した |
片想い、このせつない響き。
そのせつなさの微分方程式を解こう。
問題設定は次のようである。
タロウ君はハナコちゃんに片想い。けれどもハナコちゃんはタロウ君のことはべつに好きでも嫌いでもありません。タロウ君は時刻ゼロの瞬間からハナコちゃんを追いかけて歩きだします。ハナコちゃんはタロウ君にとくに興味があるわけでもないので、タロウ君のことはお構いなしにタロウ君の方とは直角方向に歩きだします。ふたりの歩くスピードは同じだとしたら、しばらくたったあとふたりの距離はどのくらい縮まりますか?
やはり散文で書くと不正確なので、数学の問題として書いたら以下のよう。
XY 平面上に2点 P, Q があります。点 Q は時刻 t=0 に原点 (0,0) にあり, 速さ v で Y 軸の正の方向に動きます。一方の点 P は時刻 t=0 に X 軸上の点 (L,0) にあり, 速さ v で, 常に点 Q の方向に向かって動きます。すなわち点 P の速度ベクトルは, 常にベクトル PQ と平行で, かつ大きさが v のベクトルです。このとき点 P が動く軌跡を求め, さらに十分時間がたったときの点 P と点 Q との間の距離を求めなさい。
ハナコちゃんの位置が時間の経過とともにどうなるかは自明である。時刻が t のときにはハナコちゃんは点 Q(0, vt) にいる。これは小学生でも分かる。問題はタロウ君の位置である。時刻 t でのタロウ君のいる位置を P(X,Y) としよう。問題はまずこの X と Y との間の関係を求めることであり、さらに十分 t が大きくなったときの PQ 間の距離を求めることである。
時刻 t におけるタロウ君の位置 P(X,Y) が、微小時間 dt を経たのちに点 P(X+dX,Y+dY) に移ったものとしよう。タロウ君の歩くスピードは v であるから、
(v dt)2 = (dX)2 + (dY)2 --- (A)
がまずなりたつ。両辺の平方根をとれば、
v dt = - [1 + (dY/dX)2]1/2 dX --- (A')
である。負号がついているのは、時間の経過とともにタロウ君はハナコちゃんに近づいていることあらわす。つぎにタロウ君の歩く向きがハナコちゃんの方を向いていなければならない。ハナコちゃんの位置が Q(0,vt) であることに注意すると、
-dX : dY = X : (vt-Y)
のような比例関係が存在することがわかる。ここで dX の前に負号がついているのは先ほどと同じ理由による。したがってこの式を vt について解いてやると、
vt = Y - X dY/dX --- (B)
を得る。基本的には式 (A') と式 (B) とを連立させればタロウ君の通る道筋が式のかたちで出てくる。その前に式 (B) の両辺を微分しよう。すると、
v dt = dY - dX dY/dX - X d(dY/dX) = - X d(dY/dX) --- (B')
となるから、式 (A') と式 (B') とを見比べて、
X d2Y/dX2 = [1 + (dY/dX)2]1/2 --- (C)
という微分方程式を得る。これがタロウ君の通るであろう軌跡をあらわす微分方程式である。この式から、タロウ君の歩く道筋は、歩くスピード v に依らないことがわかる。
この微分方程式を解くには、まず F = dY/dX とおく。すると F の満たす方程式は、
X dF/dX = (1 + F2)1/2 --- (C')
という、比較的簡単な一階の微分方程式となる。これを変数分離して、さらに公式集をみて(あるいはみなくてもよいが)積分すると、
log (X) = log ( F + (1 + F2)1/2 ) + (定数) --- (D)
となる。時刻ゼロの瞬間には、点 (L,0) にいるタロウ君は、原点 (0,0) にいるハナコちゃんに向かって歩き出すはずだから、時刻ゼロでは F = dY/dX = 0 である。したがって式 (D) の定数は log(L) でなくてはならない。よって式 (D) は、
X/L = F + (1 + F2)1/2 --- (D')
あるいはもっと変形して、
(X/L)2 - 2F(X/L) = 1 --- (D'')
と表すこともできる(単に式 (D') を二乗して平方根をはずしただけ)。さてここで F = dY/dX であったことを思い出すと、問題は
2 dY/dX = X/L - L/X --- (E)
を解くことに帰着されてしまったのが分かる。これはもう公式集などみなくても簡単に積分できて、答えは、
2Y/L = 1/2 (X/L)2 - log (X/L) + (定数) --- (F)
である。タロウ君は時刻ゼロに点 (L,0) にいたから、式 (F) の定数は -1/2 である。よってタロウ君の軌跡は、
(Y/L) = 1/4 (X/L)2 - 1/4 - 1/2 log (X/L) --- (F')
と求まった。
まあ最終的な答え (F') はとりたててそうおもしろいものでもない。正確にコンピューターでこの曲線を描かせると下のようになる。
 |
(左図の説明) ハナコちゃんは時刻 t=0 に原点 (0,0) にいる。タロウ君は時刻 t=0 に X 軸上の点 (L,0) にいる。 ハナコちゃんは Y 軸にそって歩く。時間 L/(2v) ごとのハナコちゃんの位置を赤色のマークで表した。 タロウ君は図のような曲線に沿って歩く。同じように時間L/(2v) ごとのタロウ君の位置を青色のマークで表した |
ではこの問題の後半部分にうつろう。それは十分時間がたったあとのタロウ君とハナコちゃんとの間の距離を求める、というものである。
時刻 t でのハナコちゃんの位置は X 軸から vt の距離にある。一方タロウ君の位置は X 軸から Y の距離にある。したがって、二人の距離の下限値は vt-Y である。ここで下限値といったのは、タロウ君はどんなに時間がたっても Y 軸にはたどりつけないからである。ただし Y 軸までの距離 X は限りなくゼロに近づく。ふたりの距離は、時間無限大の極限値として vt-Y になる。
式 (B) によれば、vt-Y は時間の関数として
vt - Y = - X dY/dX
とあらわされることがわかる。さらに式 (E) により、すでに dY/dX = 1/2 (X/L - L/X) と求まっているから、
vt - Y = 1/2 (L - X2/L)
であることがわかる。本来は X を時間の関数として陽に書き下すべきなのだろうが、いまは極限値を求めるだけでいいことにしてあるので、それは必要ない。すなわち、十分時間がたったとき X は十分小さいのはすでに自明であるから、単純に X=0 とおいて、
vt - Y = 1/2 L
が求める答えである。すなわち時間がたつと、ふたりの距離は L/2 にどんどん近くなる。このことはすでに示した図によっても明らかだろう。
この結果はなかなか興味深い。これを叙情的に解釈すると次のようになるだろうか。すなわち、ある男と女が出会った。男は女を好きになり、女にアプローチする。女は男を好きとも嫌いとも思わず、無関心でいる。そのときふたりの間の距離は、涙ぐましい男の努力にもかかわらず、いくら時間がたっても最初の距離の半分にしかならない。
あるいは逆に考えると、うざったい男がつきまとってきたとしても、自分に近づけるのは相手の領分の範囲内である、というふうにも解釈できるだろう。ふたりの間の境界線を越えては男は入ってこれない。
ふたりの距離が半分になる、というこの結果は、最初にハナコちゃんがタロウ君のいる方向とは直角方向に歩き出したということと、ふたりの歩くスピードが同じであるということの二つに依存している。その条件を変えれば答えは違ったものになる。
ちなみに数学の世界ではこの手の問題を「追跡問題」と称し、ここで得たタロウ君の軌跡のことを「追跡曲線」と呼んでいる。こうした問題はかなり古くから考えられていたらしい。おそらく微分・積分学がでてきたあたりですでに。
まあいずれにせよ、この問題は片想いのせつなさをよくあらわしているものと思う。
1999 年 9 月 1 日