The fault slips of earthquakes often propagate through complex geometries such as bends, branches, and step-overs. Exploring governing factors of such propagation is important for understanding physics of macroscopic rupture process, and various problems of rupture propagation under relatively simple condition have been studied. In addition, these studies are of great significance for disaster prevention to estimate the probability of rupture extension.
For example, when fault slip of a mega-thrust earthquake reaches the earth's surface in the subduction zone, predicting slip behavior in accretionary prism is essential to estimate the magnitude of tsunami excitation. However, even slight complexity makes problems difficult to solve numerically, and many interesting problems still remain unresolved.
In order to deal with rupture propagation in subduction zone for practical problem, it is necessary to model at least two media, free surface, and non-planar geometry or branching fault planes.
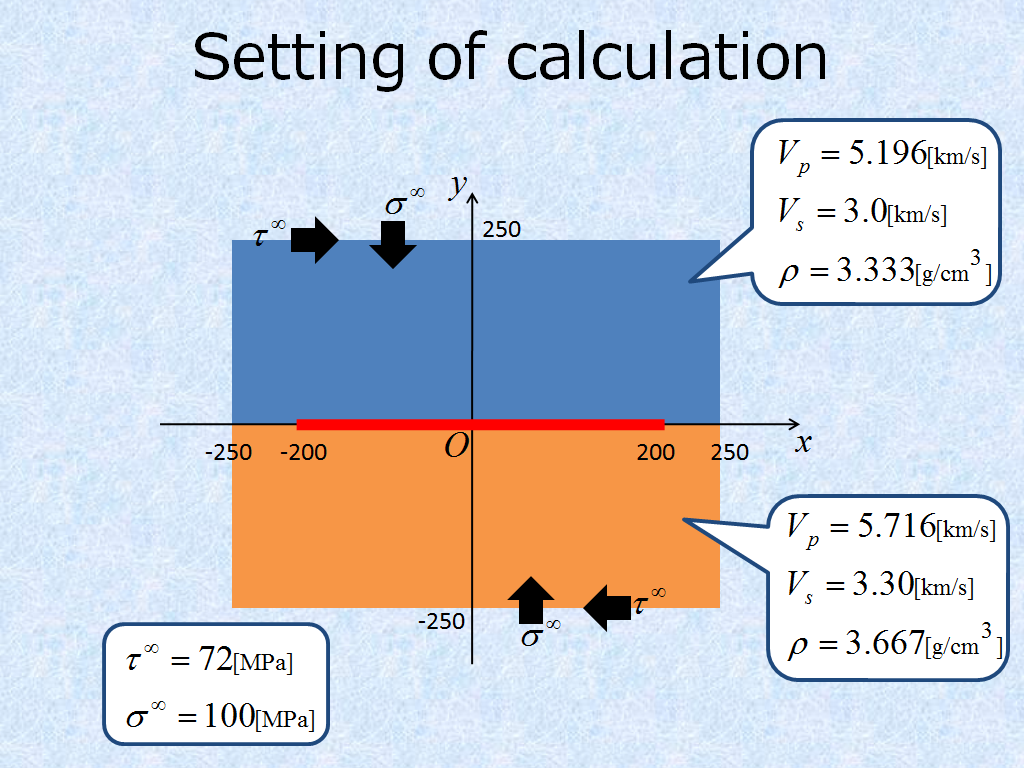
| Mode II rupture | A mode II rupture which propagates on a bimaterial interface in 2D-inplane problem(Fig.1). |
| FEM | Using the explicit Finite Element Method with split-node, which is mathematically identical to the Finite Difference Method. |
| parameter | notation | value |
|---|---|---|
| grid scale | dx | 0.5 |
| dy | 0.5 | |
| number of grids | nx | 501 |
| ny | 501 | |
| time step | dt | 0.01 |
| velocity & density of upper material |
Vp1 | 6.0 |
| Vs1 | 3.464 | |
| rho1 | 2.67 |